orbital.algorithm.template
Interface TransitionModel

Type Parameters:

A - the type of transition actions.

S - the type of transition states.

M - the class representing transitions.

All Known Subinterfaces:

GeneralSearchProblem, MarkovDecisionProblem

All Known Implementing Classes:

DelegateGeneralSearchProblem, OpenClosedGeneralSearchProblem

public interface TransitionModel

Represents a transition model. The central part underlying several other formalizations of systems consists of such a transition model.

A transition model is a mathematical model for (formal) systems with states and action-driven state changes. It forms a rewrite system, perhaps with additional probability information. A transition model is characterized by

• a state space set S.
• a set of actions A.
• sets of actions A(s)⊆A applicable in each state s∈S.
  Usually A(s) = {a∈A ¦ ∃sʹ∈S∖{⊥} P(sʹ|s,a)>0} = {a∈A ¦ τ(a)(s,⊥)≠1} = A∖τ^-1({s}×{⊥}) = τ(a)(s,·) = (τ(a)(s,·))^-1((0,1])
• the action-dependent (stochastic) transition relation
  τ:A→(S×S→[0,1])
  on S specified as either
  • deterministic transition function t:S×A(s)→S, with t(s,a) being the next state reached (for sure) when performing action a∈A(s) in state s∈S.
    τ(a)(s,sʹ) := 1 iff sʹ=t(s,a)
  • non-deterministic transition function t:S×A(s)→℘(S), such that t(s,a) is the set of next states that could be reached when performing action a∈A(s) in state s∈S.
    τ(a)(s,sʹ) := 1 ⁄ |t(s,a)| iff sʹ∈t(s,a)
  • non-deterministic transition relation T⊆S×A(s)×S, such that ⟨s,a,sʹ⟩∈T iff sʹ is a next state that could be reached when performing action a∈A(s) in state s∈S.
    τ(a)(s,sʹ) := 1 ⁄ |{sʹ∈S ¦ T(s,a,sʹ)}| iff T(s,a,sʹ)
  • stochastic transition probabilities P_a:S→[0,1]; sʹ↦P_a(sʹ|s) := P(sʹ|s,a) := P(S_t+1=sʹ|S_t=s,A_t=a) denoting the probability of reaching state sʹ∈S on taking the action a∈A(s) in state s∈S. The function P is written this way in order to remind that it has a specific probability distribution. Another possibility would be to use a combined function
    t:S×A(s)→℘(S×[0,1]); (s,a)↦{⟨sʹ,P(sʹ|s,a)⟩ ¦ sʹ∈S}
    which is more closely related to implementation issues (and thus used here), but usually considered inconvenient for the pure purpose of notation. Stochastic transitions provide the most general case of these types of transitions.
    τ(a)(s,sʹ) := P(sʹ|s,a)
  As a notation for a transition from s∈S to sʹ∈S under the action a∈A(s) with transition probability p∈[0,1] we sometimes use
  
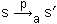
  here.

τ(a⋅b) = τ(b)∘τ(a) = ((s,sʹ) ↦ P(⋁_z∈S(S_t+2=sʹ∧S_t+1=z) | A_t+1=b,S_t=s,A_t=a)) = ((s,sʹ) ↦ ∑_z∈S τ(a)(s,z)*τ(b)(z,sʹ)) The last equation is true if the events are independent, f.ex. for a transition model satisfying the Markov property for states. In the same manner, τ(aⁿ) = τ(a)ⁿ is the (stochastic) transition relation for n transitions of fixed action a∈A. τ(a^*) = τ(a)^∞ is the transitive closure with a fixed action.

A non-deterministic transition model is a semi-Thue system with CH3 acception rules (more precise: reductions).

Note that you can as well use this interface in its raw version (i.e. without instantiating template parameters) for mere non-deterministic transitions without stochastic information by ignoring the type-restriction of TransitionModel.Transition to transition(Object,Object,Object).

Author:

André Platzer

See Also:

TransitionPath, Function, BinaryPredicate

Nested Class Summary

static interface

TransitionModel.Transition Represents (information about) a transition option during a transition model.

Method Summary

java.util.Iterator	actions(java.lang.Object state) Get the applicable actions at a state.
java.util.Iterator	states(java.lang.Object action, java.lang.Object state) Get all states reachable with any transitions from the state under a given action.
TransitionModel.Transition	transition(java.lang.Object action, java.lang.Object state, java.lang.Object statep) Get (information about) the transition from a state to another state under a given action.

Method Detail

actions

java.util.Iterator actions(java.lang.Object state)

Get the applicable actions at a state.

Intuitively, applicable actions are those that result in a valid transition. So for a state, the applicable actions are the only actions relevant for leaving that state with any transition (including transitions that lead back to the state the transition just started in).

For several reasons (including performance) it is widely recommended that

A(s) = {a∈A ¦ ∃sʹ∈S∖{⊥} P(sʹ|s,a)>0} = {a∈A ¦ τ(a)(s,⊥)≠1} = A∖τ^-1({s}×{⊥}) = τ(a)(s,·) = (τ(a)(s,·))^-1((0,1])

In fact, this is not a strict requirement, if the computation would be far too expensive. However, the TransitionModel implementation would then have to deal with cases where an action was chosen that has later been found out to be inapplicable, contrary to the initial guess of actions(Object). Since this may result in rather messy implementations, relieving this requirement should generally be limited to very specific and well documented cases.

Parameters:

state - the state s∈S whose applicable actions to determine.

Returns:

A(s)⊆A, a list of alternative actions applicable in the state s∈S. The order of the list can be decisive because for actions with equal costs the first will be preferred.

See Also:

GreedyProblem.nextCandidates(java.util.List)

Preconditions:

s∈S

Postconditions:

RES=A(s)⊆A

states

java.util.Iterator states(java.lang.Object action,
                          java.lang.Object state)

Get all states reachable with any transitions from the state under a given action.

Intuitively, those are the only relevant states which can be reached by any transitions (from the given state under the given action) at all.

For performance reasons it is recommended that this method does only return those states sʹ∈S that can truely be reached (i.e. where P(sʹ|s,a) > 0, i.e. sʹ ∈ {s}∘τ(a) = {sʹ∈S ¦ τ(a)(s,sʹ)>0}). Although this is not strictly required if it would be too expensive to determine.

Note that the resulting iterator will never be empty since the transition probabilities sum up 1 (or integrate to 1 in the case of a continuous transition probability distribution), even though the next state may not differ from the previous state.

Parameters:

action - the action a∈A(s) that must be applicable in state s∈S.

state - the state s∈S.

Returns:

a list of states sʹ∈S that could be reached when performing the action a in the state s.

Throws:

InapplicableActionException - if a∉A(s) is not applicable in state s.

Preconditions:

s∈S ∧ a∈A(s)

Postconditions:

RES ⊇ {s}∘τ(a) ∧ RES.hasNext()

transition

TransitionModel.Transition transition(java.lang.Object action,
                                      java.lang.Object state,
                                      java.lang.Object statep)

Get (information about) the transition from a state to another state under a given action.

This central method specifies the central action-dependent (stochastic) transition relation

τ:A→(S×S→[0,1])

on S. With transitions specified by τ(a)(s,sʹ)

In usual cases, implementations can assume that action stems from some call to actions(Object), and statep is obtained from states(Object,Object).

Parameters:

action - the action a∈A(s) that must be applicable in state s∈S.

state - the source state s∈S prior to the transition.

statep - the resulting state sʹ∈S after the transition took place.

Returns:

τ(a)(s,sʹ) which is the probability P(sʹ|s,a) of reaching state sʹ∈S when performing action a∈A(s) in the state s∈S. Usually represented as a transition which may contain additional information.

Throws:

InapplicableActionException - if a∉A(s) is not applicable in state s.

Preconditions:

s,sʹ∈S ∧ a∈A(s)

Postconditions:

RES=τ(a)(s,sʹ)∈[0,1] (more precisely RES.getProbability()=τ(a)(s,sʹ)) ∧ ∑_sʹ∈S τ(a)(s,sʹ) = 1