orbital.algorithm.template
Class DelegateGeneralSearchProblem

java.lang.Object
  orbital.algorithm.template.DelegateGeneralSearchProblem

All Implemented Interfaces:

java.io.Serializable, AlgorithmicProblem, GeneralSearchProblem, MarkovDecisionProblem, TransitionModel

public abstract class DelegateGeneralSearchProblem
extends java.lang.Object
implements GeneralSearchProblem, java.io.Serializable

Delegates to a GeneralSearchProblem.

For examples, this class may be used as a base class for implementing Decorators, like Decorator restricting neighbourhood by preselecting more promising actions. Either filter neighbours randomly, or select best according to an inexpensive evaluation function, or use a combined approach.

Author:

André Platzer

See Also:

Serialized Form

Structure:

delegates problem:GeneralSearchProblem

Nested Class Summary

Nested classes/interfaces inherited from interface orbital.algorithm.template.GeneralSearchProblem

GeneralSearchProblem.Transition

Nested classes/interfaces inherited from interface orbital.algorithm.template.MarkovDecisionProblem

MarkovDecisionProblem.DefaultTransition

Constructor Summary

DelegateGeneralSearchProblem(GeneralSearchProblem problem)

Method Summary

java.util.Iterator	actions(java.lang.Object param1) Get the applicable actions at a state.
MutableFunction	getAccumulatedCostFunction() Get the accumulated cost function.
protected GeneralSearchProblem	getDelegatee() Get the value of problem.
java.lang.Object	getInitialState() Get the initial state of the problem.
boolean	isSolution(java.lang.Object param1) Check whether the given state is a goal state (a valid solution to the problem).
protected void	setDelegatee(GeneralSearchProblem v) Set the value of problem.
java.util.Iterator	states(java.lang.Object param1, java.lang.Object param2) Get all states reachable with any transitions from the state under a given action. Deterministic case (will only return one single transition per action).
TransitionModel.Transition	transition(java.lang.Object param1, java.lang.Object param2, java.lang.Object param3) Get (information about) the transition from a state to another state under a given action. Deterministic case.

Methods inherited from class java.lang.Object

clone, equals, finalize, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Constructor Detail

DelegateGeneralSearchProblem

public DelegateGeneralSearchProblem(GeneralSearchProblem problem)

Method Detail

getDelegatee

protected GeneralSearchProblem getDelegatee()

Get the value of problem.

Returns:

value of problem.

setDelegatee

protected void setDelegatee(GeneralSearchProblem v)

Set the value of problem.

Parameters:

v - Value to assign to problem.

actions

public java.util.Iterator actions(java.lang.Object param1)

Description copied from interface: GeneralSearchProblem

Get the applicable actions at a state.

Intuitively, applicable actions are those that result in a valid transition. So for a state, the applicable actions are the only actions relevant for leaving that state with any transition (including transitions that lead back to the state the transition just started in).

For several reasons (including performance) it is widely recommended that

A(s) = {a∈A ¦ ∃sʹ∈S∖{⊥} P(sʹ|s,a)>0} = {a∈A ¦ τ(a)(s,⊥)≠1} = A∖τ^-1({s}×{⊥}) = τ(a)(s,·) = (τ(a)(s,·))^-1((0,1])

In fact, this is not a strict requirement, if the computation would be far too expensive. However, the TransitionModel implementation would then have to deal with cases where an action was chosen that has later been found out to be inapplicable, contrary to the initial guess of TransitionModel.actions(Object). Since this may result in rather messy implementations, relieving this requirement should generally be limited to very specific and well documented cases.

Searching often does not explicitly refer to the actions taken, but they usually form the relevant part of a solution.

Note: the return-type is Iterator in order to increase space efficiency for problems with a good expand-on-demand behaviour. Additionally, this enables implementations to use do/undo for expanding states. Implementations can either

• conservatively provide an iterator over a list that has been explicitly constructed.
• explicitly implement and provide a problem-specific iterator that constructs the actions leading to successor states on demand.
• or use the StreamMethod connector to provide an implicit yet constructive iterator in a very simple way.

Also note that if an implementation of GeneralSearchProblem.states(Object,Object) wants to optimize memory performance for the cost of limiting it to search algorithms based on depth-first search, then it can apply the do/undo technique. Alternatively, if applicable actions can be determined quickly but constructing the resulting states is expensive, the (usual) approach of lazy state construction can be used. In order to achieve this, let GeneralSearchProblem.actions(Object) return actions, without constructing any states. Then GeneralSearchProblem.states(Object,Object) performs lazy construction of resulting states on every call. However, this technique is not that powerful as do/undo, and it is less useful if the calculation of costs depends on the specific resulting states anyway. Nevertheless, it is much more simple to implement.

Specified by:

actions in interface GeneralSearchProblem

Specified by:

actions in interface TransitionModel

Parameters:

param1 -

Returns:

See Also:

GeneralSearchProblem.actions(Object)

getInitialState

public java.lang.Object getInitialState()

Description copied from interface: GeneralSearchProblem

Get the initial state of the problem.

Note that a single initial state is no restriction since one can always introduce 0-cost transitions from a single artificial initial state to a set of true initial states without affecting the search problem.

Make sure that this method consistently returns the initial state even for repeated invocations, since some iterative search algorithms may rely on this feature.

Specified by:

getInitialState in interface GeneralSearchProblem

Returns:

See Also:

GeneralSearchProblem.getInitialState()

getAccumulatedCostFunction

public MutableFunction getAccumulatedCostFunction()

Description copied from interface: GeneralSearchProblem

Get the accumulated cost function.

This function encapsulates read write access to the accumulated cost values. Search algorithms can accumulate cost for states by setting g(s) to the accumulate cost value, and later query that accumulate cost value again, by applying g.

The most simple way of providing such an accumulated cost function g, is to enrich states with a (private) field for accumulated cost that is accessible via g. So you can simply use S×R as states instead of S for storing accumulated cost values.

Since search algorithms may invoke this method several times, it should not perform too slow. So consider returning a single pre-initialized instance of the accumulate cost function.

Note that accumulated cost functions usually do not need to be cloned.

Specified by:

getAccumulatedCostFunction in interface GeneralSearchProblem

Returns:

See Also:

GeneralSearchProblem.getAccumulatedCostFunction()

states

public java.util.Iterator states(java.lang.Object param1,
                                 java.lang.Object param2)

Description copied from interface: GeneralSearchProblem

Get all states reachable with any transitions from the state under a given action.

Intuitively, those are the only relevant states which can be reached by any transitions (from the given state under the given action) at all.

For performance reasons it is recommended that this method does only return those states sʹ∈S that can truely be reached (i.e. where P(sʹ|s,a) > 0, i.e. sʹ ∈ {s}∘τ(a) = {sʹ∈S ¦ τ(a)(s,sʹ)>0}). Although this is not strictly required if it would be too expensive to determine.

Note that the resulting iterator will never be empty since the transition probabilities sum up 1 (or integrate to 1 in the case of a continuous transition probability distribution), even though the next state may not differ from the previous state.

Deterministic case (will only return one single transition per action).

Specified by:

states in interface GeneralSearchProblem

Specified by:

states in interface TransitionModel

Parameters:

param1 -

param2 -

Returns:

See Also:

GeneralSearchProblem.states(Object, Object)

transition

public TransitionModel.Transition transition(java.lang.Object param1,
                                             java.lang.Object param2,
                                             java.lang.Object param3)

Description copied from interface: GeneralSearchProblem

Get (information about) the transition from a state to another state under a given action.

This central method specifies the central action-dependent (stochastic) transition relation

τ:A→(S×S→[0,1])

on S. With transitions specified by τ(a)(s,sʹ)

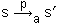
In usual cases, implementations can assume that action stems from some call to TransitionModel.actions(Object), and statep is obtained from TransitionModel.states(Object,Object).

Deterministic case. Will only return ≠0 for the unique sʹ = t(s,a). So the only true information obtained is the immediate action cost of the transition, plus any (optional) problem-specific additional information.

Specified by:

transition in interface GeneralSearchProblem

Specified by:

transition in interface TransitionModel

Parameters:

param1 -

param2 -

param3 -

Returns:

See Also:

GeneralSearchProblem.transition(Object, Object, Object)

isSolution

public boolean isSolution(java.lang.Object param1)

Description copied from interface: MarkovDecisionProblem

Check whether the given state is a goal state (a valid solution to the problem).

Optional variation: Search algorithms generally seek out for one single solution. In order to find all solutions to a problem, simply let this method store solutions and return false instead, until enough solutions have occurred. However, expanding solution nodes should result in an empty list at some time to ensure termination, then.

Specified by:

isSolution in interface MarkovDecisionProblem

Parameters:

param1 -

Returns:

See Also:

MarkovDecisionProblem.isSolution(Object)