|
⇓ Download ⇓
or get Source or read Book or watch Videos and follow Tutorial |
Overview
|
Differential dynamic logic (dL) [5,7,27,47] is a logic for specifying and verifying hybrid systems combining discrete and continuous dynamical systems.
Such hybrid systems combine discrete dynamics, e.g., for representing the instantaneous change of computer decisions with continuous dynamics represented as differential equations, e.g., for the continuous motion of a car or aircraft.
The purpose of dL is that this logic can be used to describe/specify and prove/verify correctness properties for hybrid systems given operationally as |
|
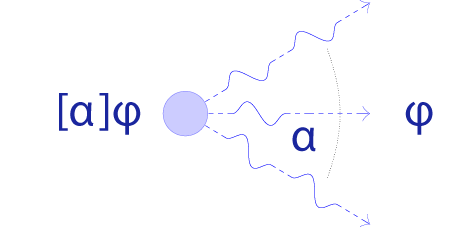
The basic idea for dL formulas is that a dL formula of the form [α]φ expresses that the hybrid system α is always within region φ, i.e., all states reachable by following the transitions of hybrid system α satisfy the formula φ. Dually, the dL formula <α>φ expresses that the hybrid system α is able to reach region φ, i.e., there is a state reachable by following the transitions of hybrid system α that satisfies the formula φ. In either case, the hybrid system α is a hybrid program describing what the dynamical system does over time. Using other propositional connectives, one can state the following dL formula
 |
dL formulas of the form φ -> [α]ψ are like a Hoare triple but for hybrid systems. dL is more flexible than Hoare calculus, because formulas of other shapes are also supported by dL. For example, the following dL formula expresses that in every initial state satisfying precondition φ there is a way of running hybrid system α to finally reach a state satisfying the postcondition ψ:
Differential dynamic logic formulas can also nest these operators arbitrarily, also with other propositional operators or quantifiers. For example, the following dL formula expresses that if all runs of hybrid system α satisfy formula φ, then all runs of hybrid system α also satisfy formula ψ:
In much the same way as finite automata can be represented as while-programs, or timed automata have a notation as real-time programs, hybrid automata can be represented as hybrid programs. Essentially, hybrid programs are what you get when you add continuous evolutions as a primitive operation to conventional discrete programs or, in fact, your favorite programming language. dL and hybrid programs thereby benefit from compositionality principles of logic and programming languages.
Note: LaTeX typesets dL as follows:
\text{\upshape\textsf{d{\kern-0.05em}L}}
Syntax
|
The syntax of the differential dynamic logic dL shown here uses slightly simplified notation in comparison to the ASCII notation in KeYmaera X. |
Operators
and Cheat Sheet |
| Formulas of dL, with typical names φ and ψ, are defined by the following syntax | ||
| φ ::= | \forall x φ | Universal quantifier: for all real values of x, formula φ holds |
| \exists x φ | Existential quantifier: for some real value of x, formula φ holds | |
| [α] φ | After all runs of hybrid program α, formula φ holds (safety) | |
| <α> φ | There is at least one run of hybrid program α, after which formula φ holds (liveness) | |
| !φ | Negation (not) | |
| φ & ψ | Conjunction (and) | |
| φ | ψ | Disjunction (or) | |
| φ -> ψ | Implication (implication) | |
| φ <-> ψ | Biimplication (equivalence) | |
| t>=s | Comparison of real arithmetic terms (likewise =,>,<,<=,!=) | |
The behavior of the hybrid system α is specified as a hybrid program, which is a program notation for hybrid systems.
| Hybrid programs, with typical names α and β, are defined by the following syntax | ||
| α ::= | α; β | Sequential composition following β after α has finished |
| α ++ β | Nondeterministic choice following either α or β | |
| α* | Nondeterministic repetition, repeating α arbitrarily often including 0 times | |
| x:=t | Discrete assignment/jump assigning the value of t to x | |
| {x'=t,y'=s & Q} | Continuous evolution along differential equation system x'=t,y'=s with terms t,s, optionally with evolution domain constraint Q. | |
| ?Q | Test whether formula Q is true in current state (otherwise abort) | |
| where Q is a formula usually in first-roder real arithmetic. | ||
Verification
|
Verifying correct functioning of hybrid systems amounts to proving corresponding formulas in differential dynamic logic dL using the dL proof calculus [5,7,27,47]. These dL formulas state the desired correctness properties of the hybrid systems under consideration, including safety, liveness, reactivity, and controllability properties. For showing that these systems operate as expected, there is a logical proof calculus as a sequent calculus [5,7] and as a Hilbert calculus [27,47] that are implemented in the theorem provers KeYmaera and its successor KeYmaera X. |
Operators |
Case studies for using differential dynamic logic to verify complex physical systems include studies for the European Train Control System (ETCS) [16] and verification of collision avoidance in aircraft collision avoidance maneuvers [15] as well as the next-generation Airborne Collision Avoidance System ACAS X [49], mobile robot navigation [51], and surgical robots [31].
Differential Invariants, Variants, Ghosts and Cuts
|
The differential equation verification technology for differential dynamic logics is based on differential invariants [8,11] that define an induction principle for differential equations [27,26,47,52,56] based on analyzing the local rate of change of truth in differential form, instead of analyzing its often significantly more complicated solution. Differential variants are a dual proof principle that can be used to prove liveness and progress properties of differential equations without having to solve them [11,18,58]. Differential cuts successively prove additional invariants for differential equations that are available during the dynamics, which are useful to accumulate knowledge about the behavior of a differential equation [8,11,27]. Differential ghosts add differential equations for new ghost variables to the existing system of differential equations enabling reasoning about the historical evolution of ODE systems in integral form [28,26]. They have been implemented in KeYmaera and KeYmaera X as well. |
|
All true algebraic invariants of differential equations are provable in differential dynamic logic [52] from these reasoning principles, and completeness even for analytic invariants with Noetherian functions [56]. In fact, all true real arithmetic invariants of differential equations are provable and all false ones disprovable in differential dynamic logic, leading to a purely logical decision procedure [52], and completeness even for semianalytic invariants [56].
Furthermore, every true bounded open safety or bounded liveness or existence property of compact initial value problems can be proved in differential dynamic logic [64].
Details and Extensions
This page only shows the simplest version of a simple differential dynamic logic. Differential dynamic logic is described in more detail in the literature [7,27,26,18,47,50,56]. A succinct readable comparison of some of the most important extensions of differential dynamic logic appeared at ABZ 2023 [61]. For more details follow this overview of logics for dynamical systems. Extensions of differential dynamic logic include the following:
- The KeYmaera X theorem prover for hybrid systems implements the dL calculus [47].
- There is an extension called quantified differential dynamic logic (QdL) [19], with which distributed hybrid systems can be verified. This is the first formal verification approach for (dynamic/reconfigurable) distributed hybrid systems, in which participants may appear and disappear during the system evolution. QdL is implemented in KeYmaera.
- The extension differential game logic (dGL) provides specification and verification for hybrid games [44,48].
- There is an extension called stochastic differential dynamic logic (SdL) [22], with which stochastic hybrid systems can be verified.
- Publications related to dL
- There is an extension called differential-algebraic dynamic logic (DAL) for more general differential-algebraic programs [8]
- ODE verification technology for differential dynamic logic is based on differential invariants [8,10,13,52,56], which are formulas that remain true along the dynamics of the hybrid system and its differential equations.
- There is a temporal extension called differential temporal dynamic logic (dTL) [4]. Also see further details and extensions in a book [18].
Differential dynamic logic itself has been originally introduced in 2007 [5] with the main results in a journal in 2008 [7]. A hybrid-nominal version of differential dynamic logic has been published at HyLo'06 [1].
Implementations
Differential dynamic logic has been implemented as a specification and verification logic in a range of different theorem provers, some dedicated to the differential dynamic logic family and others embedded in general purpose theorem provers.
- Dedicated: Differential dynamic logic and differential game logic implementation in new KeYmaera X theorem prover via uniform substitution prover microkernel [43]
- Dedicated: (Quantified) differential dynamic logic implementation in experimental KeYmaeraD theorem prover [24]
- Dedicated: Differential dynamic logic implementation in original KeYmaera 1-4 theorem prover [12]
- Deep Embedded: Differential dynamic logic formalized in Isabelle/HOL [46]
- Deep Embedded: Differential dynamic logic formalized in Rocq [46]
- Shallow Embedded: Differential dynamic logic formalized in Isabelle/UTP [UTP]
- Shallow Embedded: Differential dynamic logic formalized in PVS [PVS]
Abstract
Hybrid systems are models for complex physical systems and are defined as dynamical systems with interacting discrete transitions and continuous evolutions along differential equations. With the goal of developing a theoretical and practical foundation for deductive verification of hybrid systems, we introduce a dynamic logic for hybrid programs, which is a program notation for hybrid systems. As a verification technique that is suitable for automation, we introduce a free variable proof calculus with a novel combination of real-valued free variables and Skolemisation for lifting quantifier elimination for real arithmetic to dynamic logic. The calculus is compositional, i.e., it reduces properties of hybrid programs to properties of their parts. Our main result proves that this calculus axiomatises the transition behaviour of hybrid systems completely relative to differential equations. In a case study with cooperating traffic agents of the European Train Control System, we further show that our calculus is well-suited for verifying realistic hybrid systems with parametric system dynamics.
Keywords: dynamic logic, differential equations, sequent calculus, axiomatisation, automated theorem proving, verification of hybrid systems
See differential dynamic logic in the Journal of Automated Reasoning 2008 [7] and its uniform-substitution version in the Journal of Automated Reasoning 2017 [47].
Selected Publications
The canonical references on this approach are [7,8,27,26,18,47,50,52]. A good technical survey appeared a while ago at LICS'12 [27]. Comprehensive information on dL is available in a book [18] and a textbook [50]. Also see publications on hybrid systems logic and the publication reading guide.-
André Platzer and Long Qian.
Axiomatization of compact initial value problems: Open properties.
J. ACM 72(6), pp. 41:1-41:51, 2025. © The authors
[bib | ⧉ | pdf | doi | arXiv | abstract]
-
Jonathan Hellwig and André Platzer.
A real-analytic approach to differential-algebraic dynamic logic.
In Clark Barrett and Uwe Waldmann, editors, International Conference on Automated Deduction, CADE-30, Stuttgart, Germany, Proceedings, volume 15943 of LNCS. pp. 696-714. Springer, 2025. © The author(s)
[bib | ⧉ | pdf | doi | arXiv | abstract]
-
Marvin Brieger, Stefan Mitsch and André Platzer.
Uniform substitution for dynamic logic with communicating hybrid programs.
In Brigitte Pientka and Cesare Tinelli, editors, International Conference on Automated Deduction, CADE-29, Rome, Italy, Proceedings, volume 14132 of LNCS, pp. 96-115. Springer, 2023. © The Authors
[bib | ⧉ | pdf | doi | mypdf | slides | arXiv | abstract]
-
André Platzer.
Refinements of hybrid dynamical systems logic.
In Uwe Glässer, José Creissac Campos, Dominique Méry, Philippe Palanque, editors, Rigorous State-Based Methods - 9th International Conference, ABZ 2023, Nancy, France, Proceedings. volume 14010 of LNCS. pp 3-14. Springer, 2023. © The author under exclusive license to Springer Nature
Invited paper.
[bib | ⧉ | pdf | doi | slides | SCP'25 | abstract]
-
Yong Kiam Tan, Stefan Mitsch and André Platzer.
Verifying switched system stability with logic.
In Ezio Bartocci and Sylvie Putot, editors, Hybrid Systems: Computation and Control (part of CPS Week 2022), HSCC'22. Article No. 2, pp. 1-11. ACM, 2022.
HSCC Best Paper Award and HSCC Best Repeatability Evaluation Award. © The authors
[bib | ⧉ | pdf | doi | slides | video | kyx | arXiv | artifact | abstract]
-
Yong Kiam Tan and André Platzer.
Deductive stability proofs for ordinary differential equations.
In Jan Friso Groote and Kim G. Larsen, editors, Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2021, Proceedings, Part II, volume 12652 of LNCS, pp. 181–199. Springer, 2021. © The authors
[bib | ⧉ | pdf | doi | mypdf | slides | video | kyx | arXiv | abstract]
-
Yong Kiam Tan and André Platzer.
An axiomatic approach to existence and liveness for differential equations.
Formal Aspects of Computing 33(4), pp. 461-518, 2021.
Special issue for selected papers from FM'19. © The authors
[bib | ⧉ | pdf | doi | mypdf | arXiv | FM'19 | abstract]
-
Stefan Mitsch and André Platzer.
A retrospective on developing hybrid system provers in the KeYmaera family:
A tale of three provers.
In Wolfgang Ahrendt et al., editors, Deductive Software Verification: Future Perspectives, volume 12345 of LNCS, pp. 21-64. Springer, 2020. © Springer
[bib | ⧉ | pdf | doi | abstract]
-
André Platzer and Yong Kiam Tan.
Differential equation invariance axiomatization.
J. ACM 67(1), pp. 6:1-6:66, 2020. © The authors
[bib | ⧉ | pdf | doi | slides | video | arXiv | LICS'18 | abstract]
-
Brandon Bohrer, Manuel Fernández and André Platzer.
dLɩ Definite descriptions in differential dynamic logic.
In Pascal Fontaine, editor, International Conference on Automated Deduction, CADE-27, Natal, Brazil, Proceedings, volume 11716 of LNCS, pp. 94-110. Springer, 2019. © Springer
[bib | ⧉ | pdf | doi | slides | TR | abstract]
-
André Platzer.
Uniform substitution at one fell swoop.
In Pascal Fontaine, editor, International Conference on Automated Deduction, CADE-27, Natal, Brazil, Proceedings, volume 11716 of LNCS, pp. 425-441. Springer, 2019. © The author
[bib | ⧉ | pdf | doi | mypdf | slides | Isabelle | arXiv | errata | abstract]
-
Brandon Bohrer and André Platzer.
A hybrid, dynamic logic for hybrid-dynamic information flow.
In Anuj Dawar and Erich Grädel, editors, Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS'18, pp. 115-124. ACM 2018. © The authors. Publication rights licensed to ACM
[bib | ⧉ | pdf | doi | slides | TR | abstract]
-
André Platzer and Yong Kiam Tan.
Differential equation axiomatization:
The impressive power of differential ghosts.
In Anuj Dawar and Erich Grädel, editors, Proceedings of the 33rd Annual ACM/IEEE Symposium on Logic in Computer Science, LICS'18, pp. 819-828. ACM 2018. © The authors
[bib | ⧉ | pdf | doi | slides | video | arXiv | JACM'20 | abstract]
-
Stefan Mitsch, Khalil Ghorbal, David Vogelbacher, and André Platzer.
Formal verification of obstacle avoidance and navigation of ground robots.
International Journal of Robotics Research 36(12), pp. 1312-1340, 2017. © The authors
[bib | ⧉ | pdf | doi | kyx | arXiv | abstract]
-
André Platzer.
Logical Foundations of Cyber-Physical Systems.
Springer, Cham, 2018. 659 pages. ISBN 978-3-319-63587-3.
[bib | ⧉ | doi | slides | video | book | web | errata | abstract]
-
Jean-Baptiste Jeannin, Khalil Ghorbal, Yanni Kouskoulas, Aurora Schmidt, Ryan Gardner, Stefan Mitsch, and André Platzer.
A formally verified hybrid system for safe advisories in the next-generation airborne collision avoidance system.
STTT 19(6), pp. 717-741, 2017.
Special issue for selected papers from TACAS'15. © Springer
[bib | ⧉ | pdf | doi | kyx | study | TACAS'15 | abstract]
-
André Platzer.
Differential hybrid games.
ACM Trans. Comput. Log. 18(3), pp. 19:1-19:44, 2017. © The author
[bib | ⧉ | pdf | doi | arXiv | abstract]
-
André Platzer.
A complete uniform substitution calculus for differential dynamic logic.
Journal of Automated Reasoning 59(2), pp. 219-265, 2017. © The author
[bib | ⧉ | pdf | doi | mypdf | arXiv | abstract]
-
Brandon Bohrer, Vincent Rahli, Ivana Vukotic, Marcus Völp, and André Platzer.
Formally verified differential dynamic logic.
Certified Programs and Proofs - 6th ACM SIGPLAN Conference, CPP 2017, Paris, France, January 16-17, 2017, pp. 208-221, ACM, 2017. © ACM
[bib | ⧉ | pdf | doi | slides | Isabelle | Rocq | abstract]
-
Stefan Mitsch and André Platzer.
ModelPlex: Verified runtime validation of verified cyber-physical system models.
Formal Methods in System Design 49(1), pp. 33-74. 2016.
Special issue for selected papers from RV'14. © The authors
[bib | ⧉ | pdf | doi | mypdf | RV'14 | abstract]
-
André Platzer.
Differential game logic.
ACM Trans. Comput. Log. 17(1), pp. 1:1-1:52, 2015. © The author
[bib | ⧉ | pdf | doi | arXiv | errata | abstract]
-
Nathan Fulton, Stefan Mitsch, Jan-David Quesel, Marcus Völp and André Platzer.
KeYmaera X: An aXiomatic tactical theorem prover for hybrid systems.
In Amy P. Felty and Aart Middeldorp, editors, International Conference on Automated Deduction, CADE-25, Berlin, Germany, Proceedings, volume 9195 of LNCS, pp. 527-538. Springer, 2015. © Springer
[bib | ⧉ | pdf | doi | slides | poster | tool | tooldoi | abstract]
-
André Platzer.
A uniform substitution calculus for differential dynamic logic.
In Amy P. Felty and Aart Middeldorp, editors, International Conference on Automated Deduction, CADE-25, Berlin, Germany, Proceedings, volume 9195 of LNCS, pp. 467-481. Springer, 2015. © Springer
[bib | ⧉ | pdf | doi | slides | arXiv | JAR'17 | abstract]
-
Jean-Baptiste Jeannin, Khalil Ghorbal, Yanni Kouskoulas, Ryan Gardner, Aurora Schmidt, Erik Zawadzki, and André Platzer.
A formally verified hybrid system for the next-generation airborne collision avoidance system.
In Christel Baier and Cesare Tinelli, editors, Tools and Algorithms for the Construction and Analysis of Systems - 21st International Conference, TACAS 2015, London, UK, April 11-18, 2015, Proceedings, volume 9035 of LNCS, pp. 21-36. Springer, 2015. © Springer
[bib | ⧉ | pdf | doi | study | TR | STTT'17 | abstract]
-
Jan-David Quesel, Stefan Mitsch, Sarah Loos, Nikos Aréchiga, and André Platzer.
How to model and prove hybrid systems with KeYmaera: A tutorial on safety.
STTT 18(1), pp. 67-91, 2016. © The authors
[bib | ⧉ | pdf | doi | mypdf | abstract]
-
André Platzer.
Analog and hybrid computation: Dynamical systems and programming languages.
Bulletin of the EATCS 114, 2014. © The author
Invited paper in The Logic in Computer Science Column by Yuri Gurevich.
[bib | ⧉ | pdf | eprint | abstract]
-
Stefan Mitsch and André Platzer.
ModelPlex: Verified runtime validation of verified cyber-physical system models.
In Borzoo Bonakdarpour and Scott A. Smolka, editors, Runtime Verification - 5th International Conference, RV 2014, Toronto, ON, Canada, September 22-25, 2014. Proceedings, volume 8734 of LNCS, pp. 199-214. Springer, 2014. © Springer
Best paper finalist
[bib | ⧉ | pdf | doi | slides | study | TR | FMSD'16 | abstract]
-
Jean-Baptiste Jeannin and André Platzer.
dTL2: Differential temporal dynamic logic with nested temporalities for hybrid systems.
In Stéphane Demri, Deepak Kapur and Christoph Weidenbach, editors, Automated Reasoning, 7th International Joint Conference, IJCAR 2014, Vienna, Austria, July 19-22, 2014, Proceedings, volume 8562 of LNCS, pp. 292-306. Springer, 2014. © Springer
[bib | ⧉ | pdf | doi | slides | abstract]
-
Stefan Mitsch, Jan-David Quesel and André Platzer.
Refactoring, refinement, and reasoning:
A logical characterization for hybrid systems.
In Cliff B. Jones, Pekka Pihlajasaari and Jun Sun, editors, 19th International Symposium on Formal Methods, FM'14, Singapore, Proceedings, volume 8442 of LNCS, pp. 481-496. Springer, 2014. © Springer
[bib | ⧉ | pdf | doi | slides | abstract]
-
Khalil Ghorbal and André Platzer.
Characterizing algebraic invariants by differential radical invariants.
In Erika Ábrahám and Klaus Havelund, editors, Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2014, Proceedings, volume 8413 of LNCS, pp. 279-294. Springer, 2014. © Springer
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer.
Foundations of Cyber-Physical Systems.
Lecture Notes, Computer Science Department, Carnegie Mellon University. 2013.
[bib | ⧉ | pdf | textbook | course]
-
Sarah M. Loos, David Witmer, Peter Steenkiste and André Platzer.
Efficiency analysis of formally verified adaptive cruise controllers.
In Andreas Hegyi and Bart De Schutter, editors, 16th International IEEE Conference on Intelligent Transportation Systems, ITSC'13, The Hague, Netherlands, Proceedings, 2013. © IEEE
[bib | ⧉ | pdf | doi | slides | study | abstract]
-
Stefan Mitsch, Khalil Ghorbal and André Platzer.
On provably safe obstacle avoidance for autonomous robotic ground vehicles.
In Paul Newman, Dieter Fox, and David Hsu, editors, Robotics: Science and Systems, RSS 2013. © The author
[bib | ⧉ | pdf | eprint | slides | video | study | IJRR'17 | abstract]
-
Yanni Kouskoulas, David W. Renshaw, André Platzer and Peter Kazanzides.
Certifying the safe design of a virtual fixture control algorithm for a surgical robot.
In Calin Belta and Franjo Ivancic, editors, Hybrid Systems: Computation and Control (part of CPS Week 2013), HSCC'13, Philadelphia, PA, USA, April 8-13, 2013, pp. 263-272. ACM, 2013. © ACM
[bib | ⧉ | pdf | doi | slides | study | abstract]
-
André Platzer.
Dynamic logics of dynamical systems.
arXiv:1205.4788, May 2012. Long version of LICS'12 invited tutorial.
[bib | ⧉ | pdf | arXiv | LICS'12 | abstract]
-
André Platzer.
A differential operator approach to equational differential invariants.
In Lennart Beringer and Amy Felty, editors, Interactive Theorem Proving, International Conference, ITP 2012, August 13-15, Princeton, USA, Proceedings, volume 7406 of LNCS, pp. 28-48. Springer, 2012. © Springer
Invited paper.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
The structure of differential invariants and differential cut elimination.
Logical Methods in Computer Science 8(4), pp. 1-38, 2012. © The author
[bib | ⧉ | pdf | doi | mypdf | arXiv | abstract]
-
André Platzer.
Logics of dynamical systems.
ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pp. 13-24. IEEE 2012. © IEEE
Invited paper.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
The complete proof theory of hybrid systems.
ACM/IEEE Symposium on Logic in Computer Science, LICS 2012, June 25–28, 2012, Dubrovnik, Croatia, pp. 541-550. IEEE 2012. © IEEE
[bib | ⧉ | pdf | doi | slides | TR | abstract]
-
André Platzer.
The Complete Proof Theory of Hybrid Systems.
School of Computer Science, Carnegie Mellon University, CMU-CS-11-144, November 2011.
[bib | ⧉ | pdf | LICS'12]
-
David W. Renshaw, Sarah M. Loos and André Platzer.
Distributed theorem proving for distributed hybrid systems.
In Shengchao Qin and Zongyan Qiu, editors, International Conference on Formal Engineering Methods, ICFEM'11, Durham, UK, Proceedings, volume 6991 of LNCS, pp. 356-371. Springer, 2011. © Springer
[bib | ⧉ | pdf | doi | tool | study | errata | abstract]
-
André Platzer.
The Structure of Differential Invariants and Differential Cut Elimination.
School of Computer Science, Carnegie Mellon University, CMU-CS-11-112, April 2011.
[bib | ⧉ | pdf | arXiv | LMCS'12]
-
André Platzer.
Stochastic differential dynamic logic for stochastic hybrid programs.
In Nikolaj Bjørner and Viorica Sofronie-Stokkermans, editors, International Conference on Automated Deduction, CADE-23, Wroclaw, Poland, Proceedings, volume 6803 of LNCS, pp. 446-460. Springer, 2011. © Springer
[bib | ⧉ | pdf | doi | slides | TR | abstract]
-
André Platzer.
Logic and compositional verification of hybrid systems.
In Ganesh Gopalakrishnan and Shaz Qadeer, editors, Computer Aided Verification, CAV 2011, Snowbird, UT, USA, Proceedings, volume 6806 of LNCS, pp. 28-43. Springer, 2011. © Springer
Invited tutorial.
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
Quantified differential invariants.
In Emilio Frazzoli and Radu Grosu, editors, Proceedings of the 14th ACM International Conference on Hybrid Systems: Computation and Control, HSCC 2011, Chicago, USA, April 12-14, pp. 63-72. ACM, 2011. © ACM
[bib | ⧉ | pdf | doi | slides | abstract]
-
André Platzer.
Quantified differential dynamic logic for distributed hybrid systems.
In Anuj Dawar and Helmut Veith, editors, Computer Science Logic, 19th EACSL Annual Conference, CSL 2010, Brno, Czech Republic, August 23-27, 2010. Proceedings, volume 6247 of LNCS, pp. 469-483. Springer, 2010. © Springer
[bib | ⧉ | pdf | doi | slides | TR | LMCS'12 | abstract]
-
André Platzer.
Logical Analysis of Hybrid Systems:
Proving Theorems for Complex Dynamics.
Springer, Heidelberg, 2010. 426 pages. ISBN 978-3-642-14508-7.
[bib | ⧉ | doi | book | web | errata | abstract]
-
André Platzer.
Differential dynamic logic:
Automated theorem proving for hybrid systems.
Künstliche Intelligenz 24(1), pp. 75-77, 2010. © Springer
Invited paper.
[bib | ⧉ | doi | abstract]
-
André Platzer and Jan-David Quesel.
European Train Control System: A case study in formal verification.
In Karin Breitman and Ana Cavalcanti, editors, 11th International Conference on Formal Engineering Methods, ICFEM'09, Rio de Janeiro, Brasil, Proceedings, volume 5885 of LNCS, pp. 246-265. Springer, 2009. © Springer
[bib | ⧉ | pdf | doi | slides | kyx | TR | old | abstract]
-
André Platzer and Edmund M. Clarke.
Formal verification of curved flight collision avoidance maneuvers: A case study.
In Ana Cavalcanti and Dennis Dams, editors, 16th International Symposium on Formal Methods, FM, Eindhoven, Netherlands, Proceedings, volume 5850 of LNCS, pp. 547-562. Springer, 2009. © Springer
FM Best Paper Award.
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer.
Verification of cyberphysical transportation systems.
IEEE Intelligent Systems 24(4), pp. 10-13, Jul/Aug, 2009. © IEEE
Invited paper.
[bib | ⧉ | doi | abstract]
-
André Platzer and Edmund M. Clarke.
Computing differential invariants of hybrid systems as fixedpoints.
Formal Methods in System Design 35(1), pp. 98-120, 2009.
Special issue for selected papers from CAV'08. © Springer
[bib | ⧉ | pdf | doi | study | CAV'08 | abstract]
-
André Platzer and Jan-David Quesel.
KeYmaera: A hybrid theorem prover for hybrid systems.
In Alessandro Armando, Peter Baumgartner and Gilles Dowek, editors, Automated Reasoning, Fourth International Joint Conference, IJCAR 2008, Sydney, Australia, Proceedings, volume 5195 of LNCS, pp. 171-178. Springer, 2008. © Springer
[bib | ⧉ | pdf | doi | slides | tool | abstract]
-
André Platzer.
Differential Dynamic Logics:
Automated Theorem Proving for Hybrid Systems.
PhD Thesis, Department of Computing Science, University of Oldenburg, 2008.
ACM Doctoral Dissertation Honorable Mention Award in 2009.
Extended version appeared as book Logical Analysis of Hybrid Systems: Proving Theorems for Complex Dynamics, Springer, 2010.
[bib | ⧉ | pdf | eprint | slides | book | ebook | abstract]
-
André Platzer and Edmund M. Clarke.
Computing differential invariants of hybrid systems as fixedpoints.
In Aarti Gupta and Sharad Malik, editors, Computer Aided Verification, CAV 2008, Princeton, USA, Proceedings, volume 5123 of LNCS, pp. 176-189, Springer, 2008. © Springer
[bib | ⧉ | pdf | doi | slides | study | TR | FMSD'09 | abstract]
-
André Platzer and Edmund M. Clarke.
Computing Differential Invariants of Hybrid Systems as Fixedpoints.
School of Computer Science, Carnegie Mellon University, CMU-CS-08-103, Feb, 2008.
[bib | ⧉ | pdf | CAV'08]
-
André Platzer.
Differential-algebraic dynamic logic for differential-algebraic programs.
Journal of Logic and Computation 20(1), pp. 309-352, 2010.
Special issue for selected papers from TABLEAUX'07. © The author
[bib | ⧉ | pdf | doi | eprint | study | errata | TABLEAUX'07 | abstract]
-
André Platzer.
Differential dynamic logic for hybrid systems.
Journal of Automated Reasoning 41(2), pp. 143-189, 2008. © The author
[bib | ⧉ | pdf | doi | mypdf | study | abstract]
-
André Platzer.
Combining deduction and algebraic constraints for hybrid system analysis.
In Bernhard Beckert, editor, 4th International Verification Workshop, VERIFY'07, Bremen, Germany, CEUR Workshop Proceedings, 259:164-178, 2007.
[bib | ⧉ | pdf | eprint | slides | abstract]
-
André Platzer.
Differential dynamic logic for verifying parametric hybrid systems.
In Nicola Olivetti, editor, Automated Reasoning with Analytic Tableaux and Related Methods, International Conference, TABLEAUX 2007, Aix en Provence, France, July 3-6, 2007, Proceedings, volume 4548 of LNCS, pp. 216-232. Springer, 2007. © Springer
TABLEAUX Best Paper Award.
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer.
A temporal dynamic logic for verifying hybrid system invariants.
In Sergei Artemov and Anil Nerode, editors, Logical Foundations of Computer Science, International Symposium, LFCS 2007, New York, USA, Proceedings, volume 4514 of LNCS, pp. 457-471. Springer, 2007. © Springer
[bib | ⧉ | pdf | doi | slides | study | TR | abstract]
-
André Platzer.
Differential logic for reasoning about hybrid systems.
In Alberto Bemporad, Antonio Bicchi and Giorgio Buttazzo, editors, Hybrid Systems: Computation and Control, 10th International Conference, HSCC 2007, Pisa, Italy, Proceedings, volume 4416 of LNCS, pp. 746-749. Springer, 2007. © Springer
[bib | ⧉ | pdf | doi | poster | abstract]
-
André Platzer.
Differential logic for reasoning about hybrid systems.
In Alberto Bemporad, Antonio Bicchi and Giorgio Buttazzo, editors, Hybrid Systems: Computation and Control, 10th International Conference, HSCC 2007, Pisa, Italy, Proceedings, volume 4416 of LNCS, pp. 746-749. Springer, 2007. © Springer
[bib | ⧉ | pdf | doi | poster | abstract]
-
André Platzer.
Towards a hybrid dynamic logic for hybrid dynamic systems.
In Patrick Blackburn, Thomas Bolander, Torben Braüner, Valeria de Paiva and Jørgen Villadsen, editors, Proc., International Workshop on Hybrid Logic, HyLo 2006, Seattle, USA, Electr. Notes Theor. Comput. Sci. 174(6):63-77, 2007.
[bib | ⧉ | pdf | doi | slides | abstract]
For full details, please see List of Publications.
There also is a verification tool implementation of dL in a theorem prover, which is called KeYmaera [12].
 |
Any opinions, findings, and conclusions or recommendations expressed are those of the author(s) and do not necessarily reflect the views of any sponsoring institution.